A Challenging Proof of Complex Numbers: Discovering the Truth
Written on
Chapter 1: Understanding the Problem
In the realm of complex numbers, we can visualize a square in the complex plane with corners at the coordinates 1, i, -1, and -i. The task is to demonstrate that for any two complex numbers, u and v, that lie within this square, their product uv will also reside within the same area. Initially, I assumed this problem would be straightforward—how wrong I was!
When multiplying complex numbers, the polar form often simplifies the process. In this representation, a complex number is characterized by its modulus (the distance from the origin, denoted as r) and the angle it makes with the horizontal axis (θ). To multiply two complex numbers in polar coordinates, you simply multiply their moduli and add their angles together.
Given that both complex numbers have a modulus of less than 1, it follows that their product's modulus will also be less than 1, ensuring it lies within a circle of radius 1. However, this does not necessarily confirm that the product remains within the square! Thus, the challenge is greater than I initially perceived.
Exploring Specific Cases
Let’s examine a scenario where one of the complex numbers, say u, is positioned exactly at one of the square's vertices. In this case, its modulus will equal 1 and its angle could be 0°, 90°, 180°, or 270°. Consequently, the multiplication effect on the other complex number will manifest as a rotation by one of these angles.
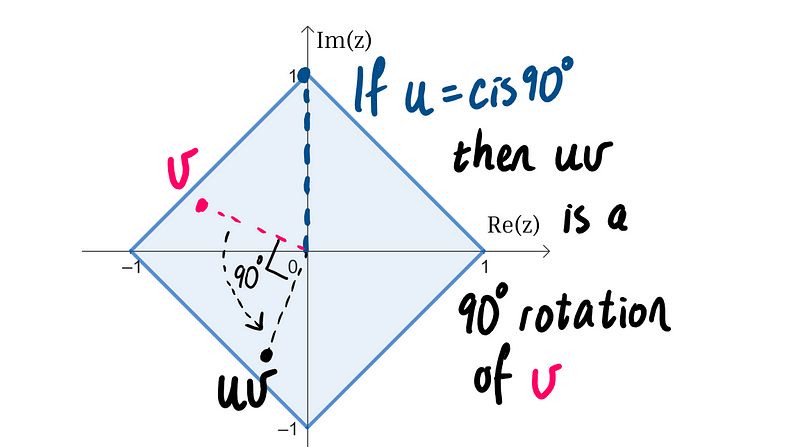
By analyzing the square’s symmetry, we observe that if v is contained within the square, then the product uv—resulting from a 90° rotation—will also fit within the square.
Utilizing Rotational Symmetry
A key insight that aids in simplifying the problem is the square's rotational symmetry of 90°. Rotating the square by this angle results in the same shape. This implies that if either complex number has an angle exceeding 90°, we can subtract a multiple of 90° without altering whether the product remains inside the square.
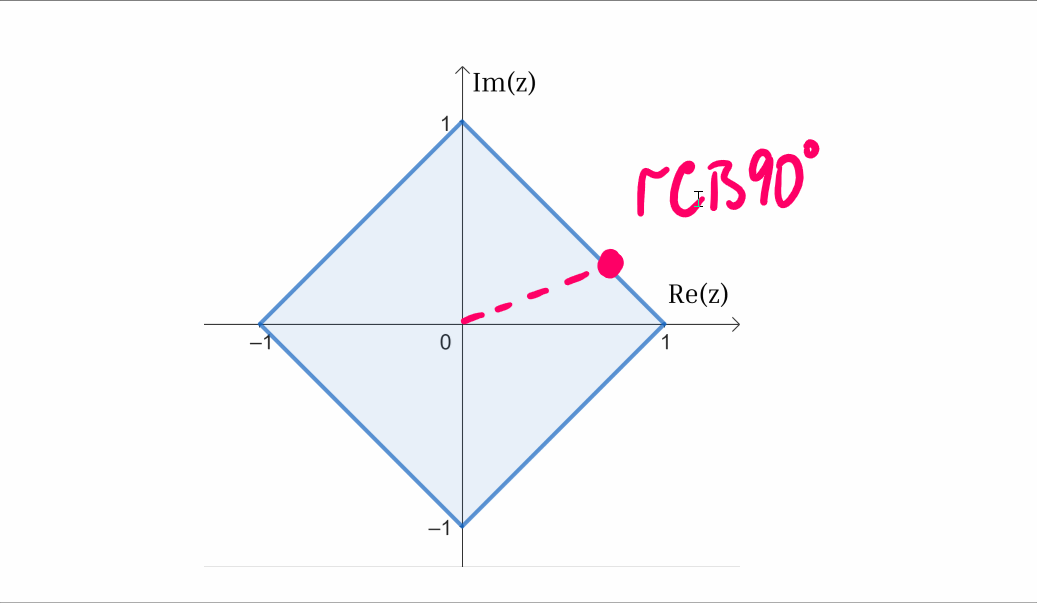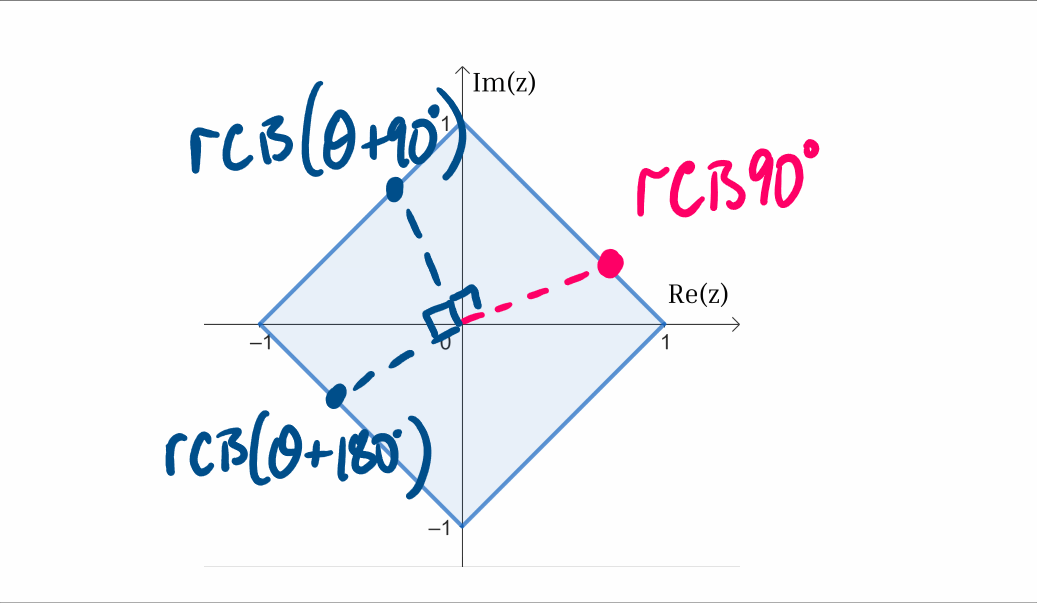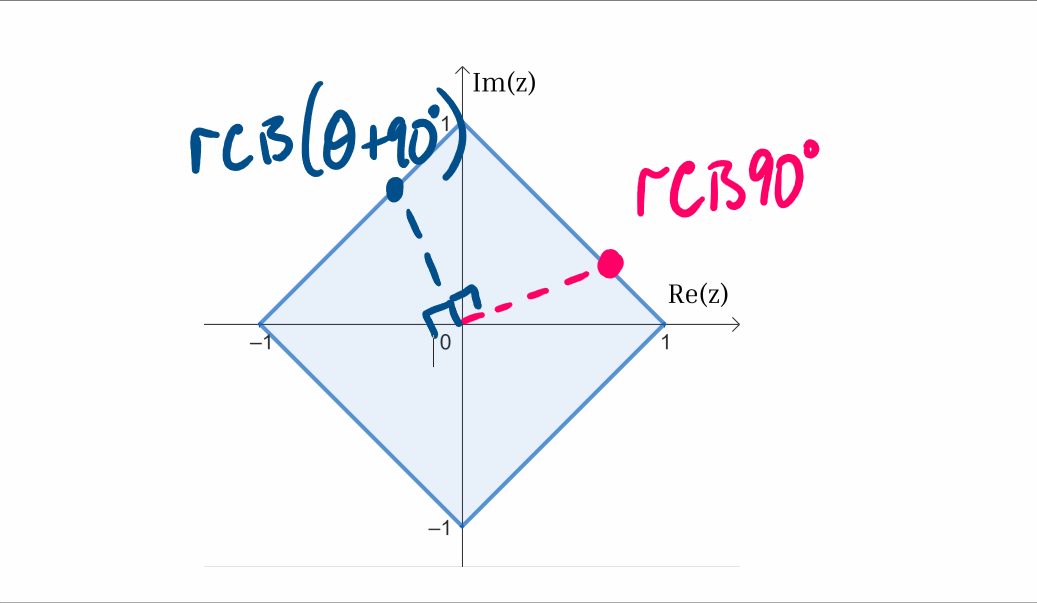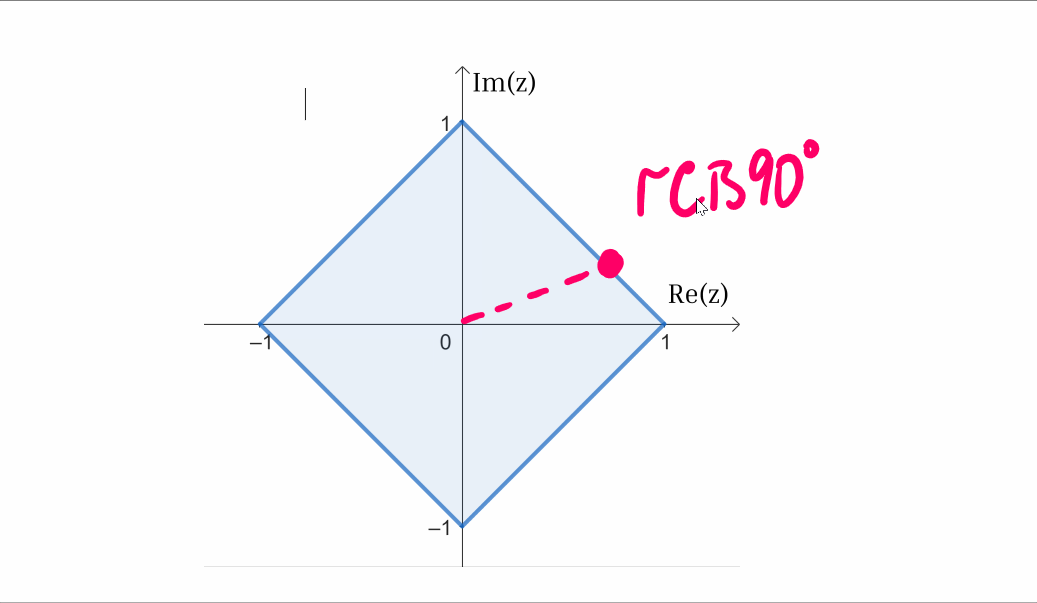
For instance, if one complex number has an angle of 150°, we can modify it to 60° (150° - 90°). If the resulting product remains inside the square, then the original product will too. This transformation streamlines our analysis to complex numbers whose angles range from 0° to 90°.
Transitioning to Rectangular Form
Surprisingly, tackling this problem in rectangular coordinates proves to be more effective. Let’s define u as a + bi and v as c + di. We can rotate both complex numbers back to the first quadrant, ensuring that a, b, c, and d are all positive.
As both u and v are confined within the square, they must also fall below the line represented by x + y = 1.
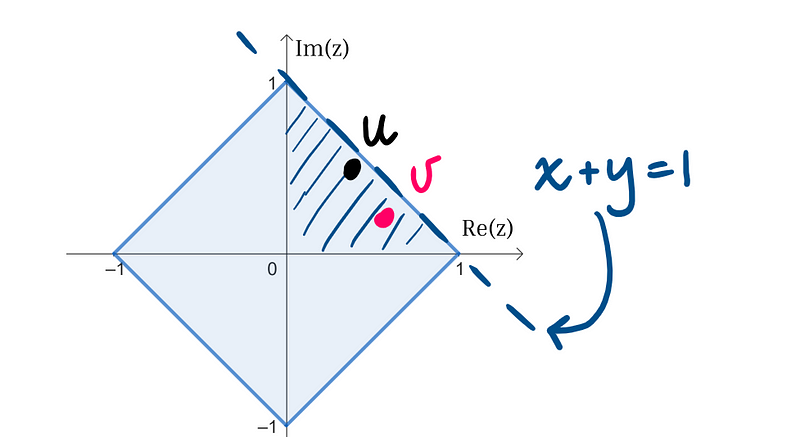
Next, we need to demonstrate that uv = (a + bi)(c + di) also lies within the square. Expanding the product reveals that uv indeed remains below the line defined by x + y = 1.
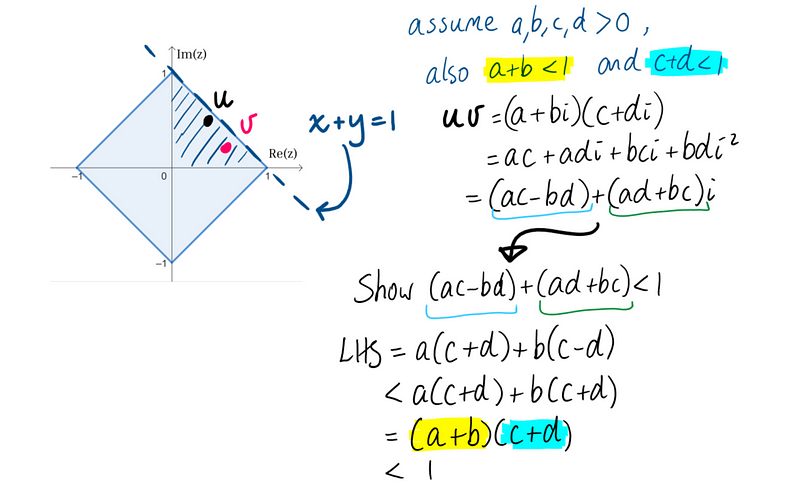
In the penultimate line, I relied on the fact that (c - d) is less than (c + d), a true statement given that c and d are both positive. However, we must remember that while u and v are in the first quadrant, the product uv could potentially land in the second quadrant.
In this case, while it is not crucial for the product to remain below the line x + y = 1, it must be shown that it stays below the line y - x = 1. Thankfully, a similar expansion method in rectangular form, combined with our prior assumptions about a, b, c, and d, suffices to prove this point.
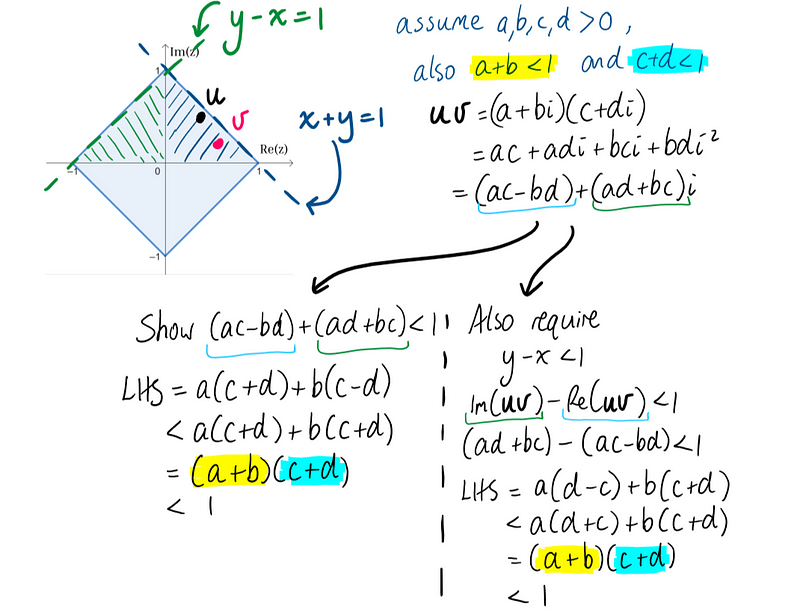
— — Q.E.D. — —
This problem, as presented, is a specific case of a broader theorem concerning regular polygons in the complex plane, specifically those with a vertex at (1,0). For further exploration, refer to this discussion on StackExchange regarding the multiplication of complex numbers within a regular polygon.
Conclusion
The mathematical exploration into complex numbers and their properties within geometric shapes reveals intricate relationships and profound insights, proving that even seemingly simple problems can harbor deep complexities.