Exploring the Enigma of the Collatz Conjecture: A Simple Yet Complex Problem
Written on
Chapter 1: Understanding the Collatz Conjecture
Welcome back to another edition of Daily Science! Today, we venture into the intriguing world of the Collatz Conjecture, a mathematical puzzle that has puzzled minds for generations.
So, what is this conjecture all about? Essentially, it involves a simple set of operations applied to any chosen number, which we can call n. To begin, select any integer. If n is even, divide it by 2. If n is odd, multiply it by 3 and add 1. This process is repeated, and it is theorized that you will eventually arrive at the number 1, which then leads to the loop of 4, 2, 1.
For instance, starting with the number 5 yields the following sequence: 5, 16 (since 5 is odd: 5*3 + 1), 8 (16/2), 4 (8/2), 2 (4/2), and finally 1 (2/2). At this point, the numbers cycle indefinitely through 4, 2, and 1.
The core of the conjecture posits that no matter which number you begin with, you will always reach 1 in a finite number of steps. The question mathematicians are grappling with is whether there exists any number that either falls into a unique loop or diverges to infinity.
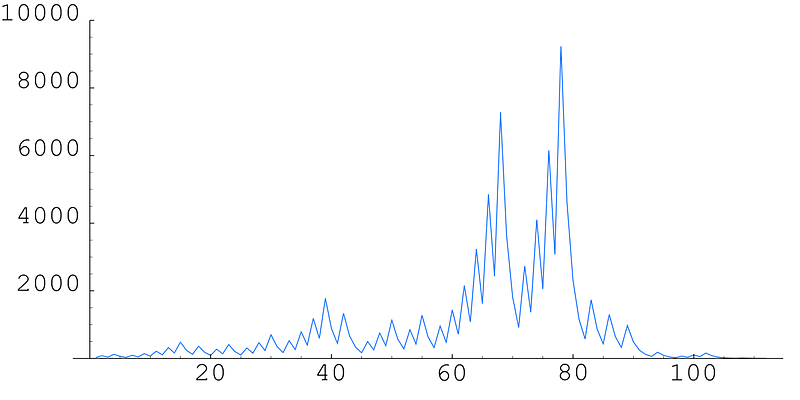
Photo by Pokipsy76 on Wikipedia - Sequence for N=27 reaching 9232 before entering the loop.
This conundrum has persisted since 1937 and remains one of the most significant unsolved problems in mathematics.
Section 1.1: The Search for Answers
How are mathematicians approaching this elusive problem? Interestingly, many young mathematicians are advised against wasting their time on this conjecture. After all, if some of the greatest minds in mathematics have been unable to crack it, how could a college student possibly succeed?
Nonetheless, those who persist often turn to computational methods to explore potential solutions, seeking patterns that could lead to answers. For instance, if a number reappears in the sequence, it indicates the presence of a closed loop. Computers have proven to be invaluable tools in this endeavor, expediting the search for solutions. Unfortunately, it appears that the Collatz Conjecture might remain unresolved.
After analyzing approximately 2^70 (around 2.95*10^21) numbers, no counterexamples have surfaced; instead, they all eventually succumb to the 4, 2, 1 loop. The closest instance of a number approaching an infinite sequence involved the enormous number 115,132,219,018,763,992,565,095,597,973,971,522,401, which required 292,000 operations before ultimately reaching the loop, as discussed in a Quora chat.
The Simplest Math Problem No One Can Solve - Collatz Conjecture
This video explores the Collatz Conjecture's complexities, showcasing its enigmatic nature and the attempts made to solve it.
Section 1.2: Insights from Research
Despite extensive efforts and rigorous computational analysis, mathematicians have yet to uncover a counterexample to the Collatz Conjecture. The first 2^70 numbers analyzed have provided substantial evidence supporting the theory that all integers ultimately converge to 1.
Researchers have noted that certain sequences feature repeated cycle lengths, hinting at the existence of closed loops. However, while these insights are noteworthy, they do not constitute a definitive or comprehensive solution.
Chapter 2: The Future of the Collatz Conjecture
Will we ever uncover the answer to this mathematical enigma? Only time will tell. Rest assured, I will keep you updated if we ever find proof or disproof of the Collatz Conjecture!
Collatz Conjecture: NOBODY Can Prove Why!!
This video delves into the challenges faced by mathematicians in proving the Collatz Conjecture, highlighting its perplexing nature.