Chapter 1: Introduction to the Puzzle

The task of summing all odd numbers that are less than 100 can be traced back to a famous anecdote about the young mathematician Johann Carl Friedrich Gauss. When challenged by his teacher to sum the integers from 1 to 100, Gauss promptly devised a clever strategy that would later contribute to his acclaim as one of history's leading mathematicians. In this exploration, we will apply a similar technique to tackle our current puzzle. For clarity, we will only consider positive integers, as including negatives would lead to an undefined outcome.

Chapter 2: Understanding the Method

To determine the sum of all odd numbers below 100, we can reframe the problem. Essentially, we want the total of all integers under 100, but excluding the even numbers. Consequently, we can arrive at our solution by deducting the sum of the even integers from the total sum of integers below 100.

To begin, we need to calculate the sum of all integers from 1 to 99. The formula for the sum of the first n integers is crucial here. We can visualize these numbers arranged in a triangular formation.

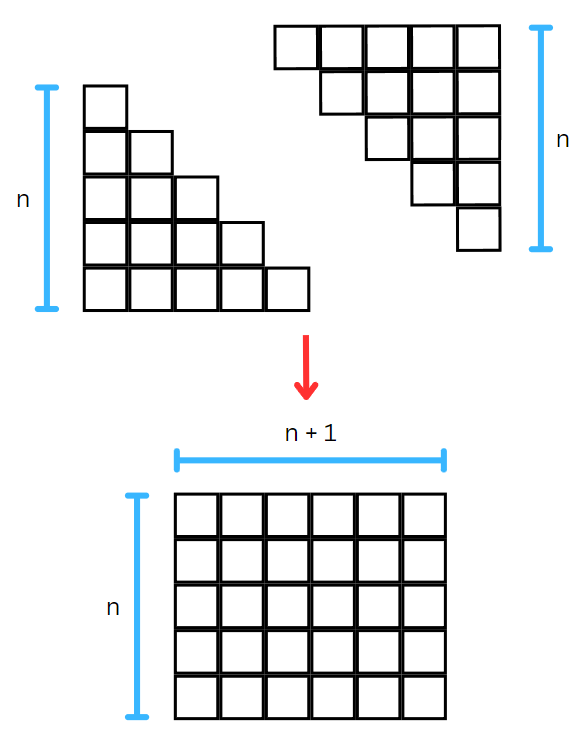
Here’s a simple example using the first five integers. By flipping this triangular arrangement and joining it with itself, we can create a rectangular configuration.

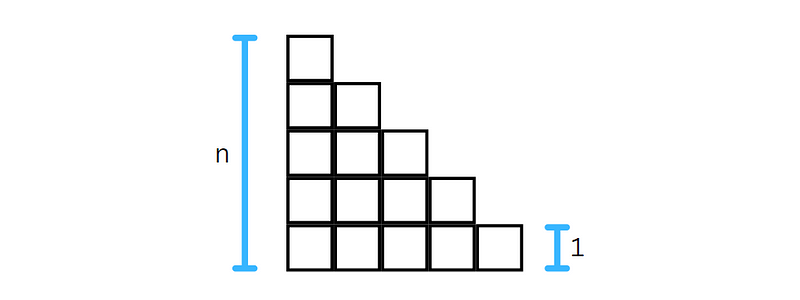
This rectangle consists of n(n + 1) squares, combining two triangular sections. Therefore, the formula to find the sum of integers from 1 to n is:

Applying this, the sum of the first 100 integers is calculated as 100 * 101 / 2, resulting in 5050.

Chapter 3: Summing the Even Numbers

Next, we focus on the sum of even numbers under 100. This series comprises 2, 4, 6, ..., 98. Notably, the sum of these even numbers can be perceived as twice the sum of the integers from 1 to 50.

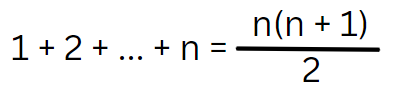
Utilizing our earlier formula, we find that the sum of numbers from 1 to 50 equals 50 * 51 / 2, which amounts to 1275. Therefore, doubling this yields 1275 * 2 = 2550.

To conclude, as previously mentioned, we can now derive the sum of all odd numbers less than 100 by subtracting the total of even numbers from the overall sum:

5050 - 2550 = 2500.

Thus, the sum of 1 + 3 + ... + 97 + 99 equals 2500.

The first video titled "How to find sum of first n odd numbers" provides a detailed explanation of this approach and additional insights.

Challenge 1: Propose an alternative method to solve this problem using the average.

Challenge 2: What would be the total of all odd numbers from 1 to 1000?

The second video, "What is the average of all the odd numbers less than 100?" explores average calculations relevant to this topic.