Chapter 1: Goldbach's Conjecture Unveiled

Goldbach’s conjecture stands as one of the most renowned unsolved dilemmas in the realm of number theory, and arguably in all of mathematics.

Christian Goldbach, on a warm summer evening in 18th-century Russia, penned a letter to Leonhard Euler, suggesting a mathematical conjecture. Even after more than 200 years, mathematicians have yet to either prove or disprove this intriguing proposition.

On June 7, 1742, the German mathematician Christian Goldbach sent his letter (Letter XLIII) to Euler, proposing that:

Every integer expressible as the sum of two primes can also be represented as the sum of any number of primes until all terms are reduced to units.

In his original proposal, Goldbach erroneously included 1 as a prime number—a convention that has since been dismissed. He also noted a secondary conjecture in the margins:

Every integer greater than 2 can be decomposed into the sum of three primes.

Euler, one of the greatest mathematicians of all time, reviewed Goldbach’s proposition and responded on June 30 of the same year. Goldbach noted that the first conjecture would naturally arise from the assertion:

Every positive even integer can be represented as the sum of two primes.

The contemporary version of Goldbach’s older conjecture is stated as follows:

Every even integer larger than 2 can be expressed as the sum of two primes.

The marginal conjecture's modern interpretation is:

Every integer exceeding 5 can be expressed as the sum of three primes.

Let’s explore this with a few examples. Consider the even number 8; it can be expressed as the sum of the primes 5 and 3. If we take a larger number, 118, it can be represented as the sum of the primes 5 and 113. In fact, there are several pairs of primes that yield 118:

5 + 113, 11 + 107, 17 + 101, 29 + 89, 47 + 71, 59 + 59.

Now, let’s examine the even larger number 65,448,866. This can also be expressed as the sum of 19 and 65,448,847, and there may be countless pairs of primes that sum to 65,448,866.

This is the essence of the Goldbach conjecture—its simplicity and ease of testing make it accessible. For larger numbers, one can easily verify the conjecture using a straightforward computer program. You can create a code in any programming language or utilize online tools to check various numbers.

If you're unfamiliar with the term "conjecture," it refers to a conclusion or proposition believed to be true based on preliminary evidence, yet lacking a formal proof or disproof.

The Goldbach conjecture, like the Collatz conjecture, has been validated for a vast range of numbers without being disproven.

To gain further insight into the Collatz conjecture, check out this video:

Chapter 2: A Simple Problem Mathematicians Can’t Resolve

In 1937, Lothar Collatz introduced his conjecture shortly after earning his doctorate. Mathematicians have since tested this conjecture extensively, with Nils Pipping verifying it for values up to n = 10^5 in 1938. T. Oliveira e Silva later expanded the search, confirming the conjecture for values up to n = 4 × 10^18 as of 2013.

The smallest number that cannot be expressed as a sum of two primes, where one prime is less than 9,781, is 3,325,581,707,333,960,528.

Even a smaller number, such as 2566, can be expressed as a sum of 37 pairs of primes:

17 + 2549, 23 + 2543, 89 + 2477, 107 + 2459, 149 + 2417, 167 + 2399, 173 + 2393, 227 + 2339, 233 + 2333, 257 + 2309, 269 + 2297, 293 + 2273, 353 + 2213, 359 + 2207, 467 + 2099, 479 + 2087, 503 + 2063, 563 + 2003, 569 + 1997, 587 + 1979, 593 + 1973, 617 + 1949, 653 + 1913, 659 + 1907, 677 + 1889, 719 + 1847, 743 + 1823, 857 + 1709, 929 + 1637, 947 + 1619, 953 + 1613, 983 + 1583, 1013 + 1553, 1193 + 1373, 1259 + 1307, 1277 + 1289, 1283 + 1283.

Impressive, isn’t it?

To visualize how all even numbers can be represented as sums of two primes, consider the Goldbach partitions shown below.

To further comprehend this conjecture, let’s discuss prime numbers. The prime number theorem suggests that for a randomly selected integer m, the likelihood of it being a prime is approximately 1/ln(m).

Therefore, if n is a large even integer and m is a number between 3 and n/2, the probability that both m and (n - m) are prime is given by:

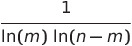
Using heuristics, the total number of ways to express a large even integer n as the sum of two odd primes can be approximated by:

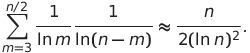
As ln(m) is significantly less than √n, this quantity approaches infinity as n increases, indicating that every large even integer likely has not just one representation but multiple representations as sums of two primes.

To test whether a number adheres to this conjecture, feel free to utilize the Python code provided below, which can be run on any online compiler:

import math

MAX = 100000

primes_list = []

def sieve_of_Sundaram():

half_MAX = MAX / 2

marked = [False] * (int(half_MAX) + 100)

for i in range(1, int((math.sqrt(MAX) - 1) / 2) + 1):

for j in range((i * (i + 1)) << 1, int(half_MAX) + 1, 2 * i + 1):

marked[j] = True

primes_list.append(2) # 2 is prime

for i in range(1, int(half_MAX) + 1):

if not marked[i]:

primes_list.append(2 * i + 1)

def findPrimes(n):

if n <= 2 or n % 2 != 0:

print("Invalid Input")

return

i = 0

while primes_list[i] <= n // 2:

diff = n - primes_list[i]

if diff in primes_list:

print(primes_list[i], "+", diff, "=", n)

return

i += 1

sieve_of_Sundaram()

findPrimes(69420)

Numerous graphical representations illustrate the number of ways to express even numbers as sums of two primes, revealing a beautiful pattern.

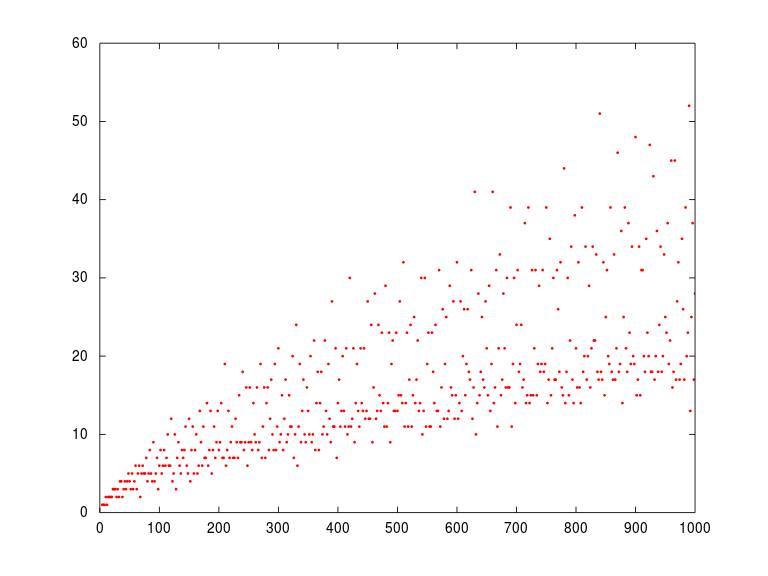
This graph showcases the various ways to express even numbers between 4 and 1000 as sums of two primes.

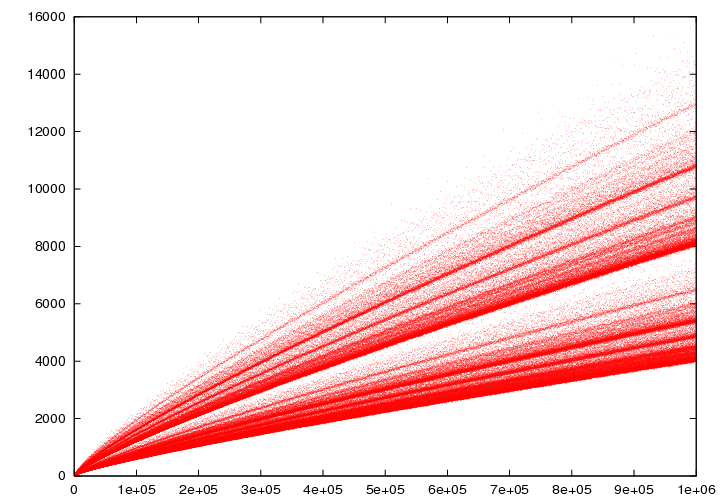
As illustrated, as n increases, the number of representations of n as the sum of two primes also grows.

The assertion “Every even integer greater than 2 can be expressed as the sum of two primes” is the common contemporary formulation of the conjecture, known as the “strong,” “even,” or “binary” Goldbach conjecture. Conversely, the “weak” Goldbach conjecture posits that “Every odd integer greater than 7 can be expressed as the sum of three odd primes.”

In 2013, Harald Helfgott proposed a proof for the weak Goldbach conjecture!

Despite centuries of scrutiny, the proof or disproof of Goldbach’s conjecture remains elusive. Although numerous numbers have been examined, there may still exist a number that contradicts the conjecture, sufficient to disprove it.

If you believe we have explored enough numbers, consider the Pólya Conjecture proposed by Hungarian mathematician George Pólya in 1919. It was disproven in 1958 by C. Brian Haselgrove, with the counter-example being 1.854 × 10^31.

This ongoing enigma reflects the nascent stage of mathematics, indicating that there is still much to discover.

For those curious about how mathematics secures your data, check out this insightful article:

This Military Technology is Being Used Everyday in Our Lives

A deep dive into how math keeps your data secure.