Chapter 1: The Essence of Limits

In this continuation of my series on learning calculus from the ground up, we delve into the concept of limits, a cornerstone of the discipline. It is crucial to grasp limits thoroughly as they are as vital to calculus as numbers are to arithmetic or shapes are to geometry. Understanding limits will enable us to navigate the complexities of calculus with greater ease.

A limit can be described as the process by which a sequence of numbers approaches a particular value. But why is this important? Consider a function like f(x) = sin(x)/x. To illustrate, let's examine its graph:

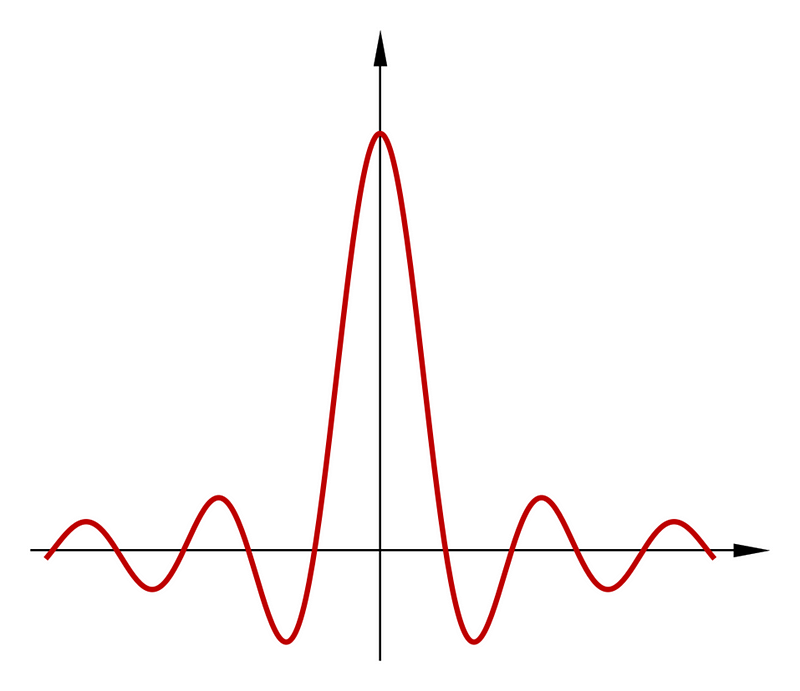
This function appears well-defined, including at x=0. However, we face a challenge: how can we define this function at x=0 when dividing by zero is mathematically prohibited? To address this, we need to consider the function separately for x approaching 0 and for x equal to 0. We can ponder if there exists a value that renders the function continuous at 0. While direct substitution of 0 is not permitted, we can let x approach 0 in the expression sin(x)/x.

A pertinent question arises: Can we mathematically quantify the idea of getting infinitely close to a number? Let's consider an infinite sequence of real numbers:

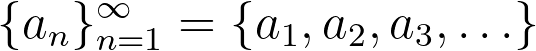
We say that a real number L serves as the limit of this sequence if, for any small number ε > 0, there exists a sufficiently large number N such that for all n greater than N, the distance between the nth element of the sequence and L is less than ε. In simpler terms, this means the sequence gets increasingly close to L. In formal mathematical terms, this can be expressed as:

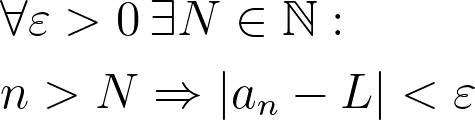
While understanding this epsilon-delta definition is not strictly necessary at this stage, hands-on problem-solving is the most effective way to grasp limits.

Limits can be denoted in two distinct manners. The first notation expresses:

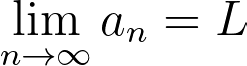
However, to use this notation, it is essential to confirm that the limit exists. Another common representation is as follows:

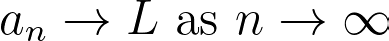
In this case, the limit may not necessarily exist; L could be infinite. Limits can be applied not just to sequences but also to functions. Thus, if f is a real-valued function and c is a real number, we denote:

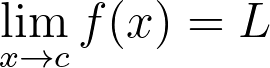
This notation signifies evaluating f at c or at a value "infinitely close to" c when direct evaluation is impossible. Ultimately, the epsilon-delta definition underpins this process.

Now, how do we compute limits? In some scenarios, the answer is straightforward. For instance, if c ≠ 0, then:

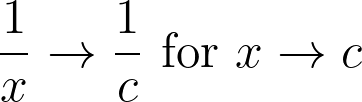
However, caution is necessary when c = 0. The function 1/x is discontinuous at this point; thus, the limit varies depending on the direction from which we approach 0. Approaching from above (the right) yields +∞, while approaching from below (the left) yields -∞.

Returning to our example with f(x) = sin(x)/x, although we cannot substitute 0 directly, we can let x approach 0 in our expression. How can we accurately determine this limit? Numerous methods exist, but they typically rely on derivatives, which we have not yet covered in this introductory discussion. Therefore, we need an alternative approach to find this limit.

Consider the sine function, which takes an angle θ as input and returns the length of the opposite side of a right triangle inscribed in the unit circle:

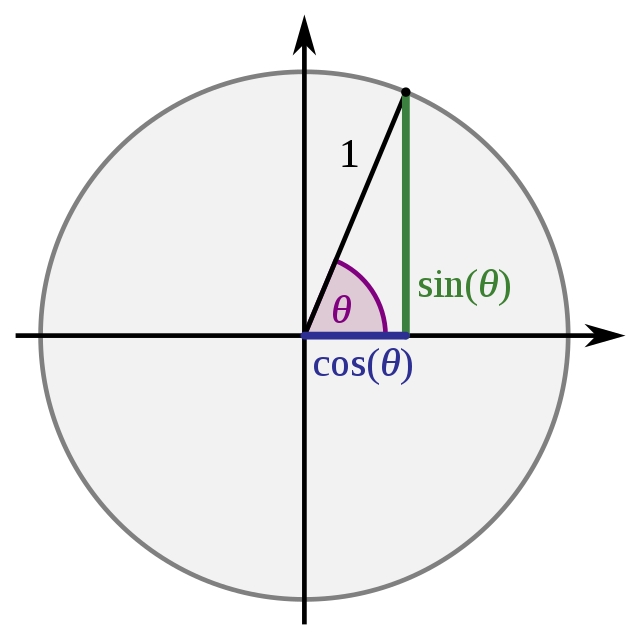
As θ approaches 0, sin(θ) also approaches 0. Notably, they do so at a comparable rate, suggesting that the ratio between the triangle's opposite side and angle θ approaches 1 as θ nears 0. We will refine this concept in future discussions using derivatives, Taylor series, and L'Hôpital's rule.

Now we can define our function:

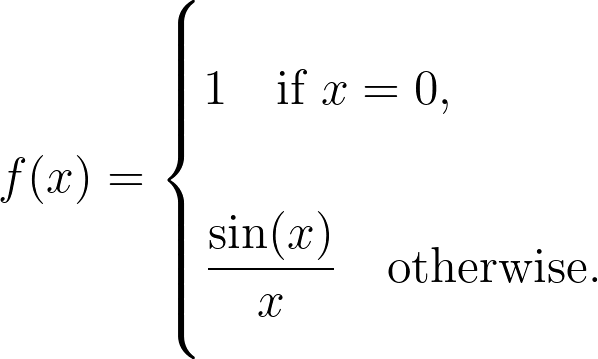
Remarkably, this function is not only continuous at 0 but also differentiable at that point. Our exploration of limits is far from complete; they are woven throughout calculus and its various branches, much like an enduring companion. As we progress through this series, we will develop techniques to calculate limits, including:

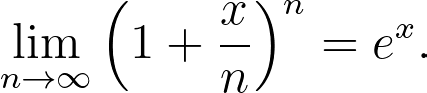
So far in this series, we have covered:

1. Functions and Continuity
2. Prerequisites for Calculus

For further exploration of these concepts, check out the following video resources:

This video provides an introduction to limits, laying the groundwork for understanding their significance in calculus.

In this video, NancyPi demonstrates how to find limits in various scenarios, reinforcing your understanding of this crucial concept.