Understanding Dedekind Numbers

What exactly is a Dedekind number? This question might have crossed your mind, and the explanation is quite simple! The answer is rooted in the realm of Boolean functions.

So, what are Boolean functions?

According to Wikipedia, a Boolean function is a function where both the inputs and outputs come from a two-element set, commonly represented as {true, false}, {0,1}, or {-1,1}.

For instance, let's examine the AND function:

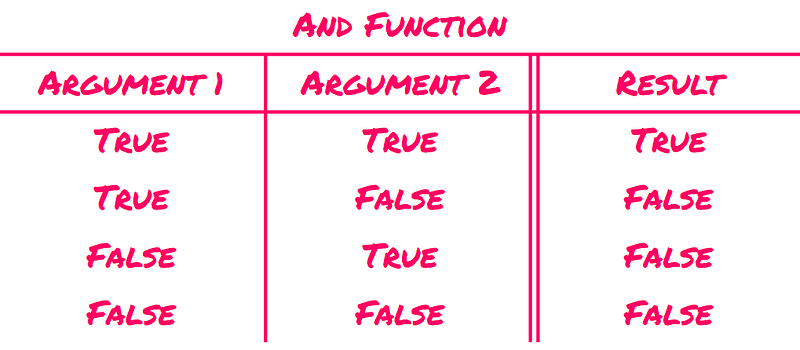
The AND Function Explained

For every combination of inputs—true and true, true and false, false and true, false and false—this function produces a singular outcome: it returns true only if both inputs are true. This concept aligns with the statement "It’s cold outside and the capital of France is Paris," which is true only when both components are accurate.

Thus, the AND function is categorized as a Boolean function since both its inputs and outputs are limited to the binary values {true, false}. Additionally, the AND function is classified as a monotonic Boolean function, meaning that changing any false input to true can only result in the output changing from false to true, never vice versa. For instance, if we change the second argument from false to true, both inputs are true (similar to the first combination), and consequently, the output is also true.

On the other hand, consider the XOR function, which does not maintain this property:

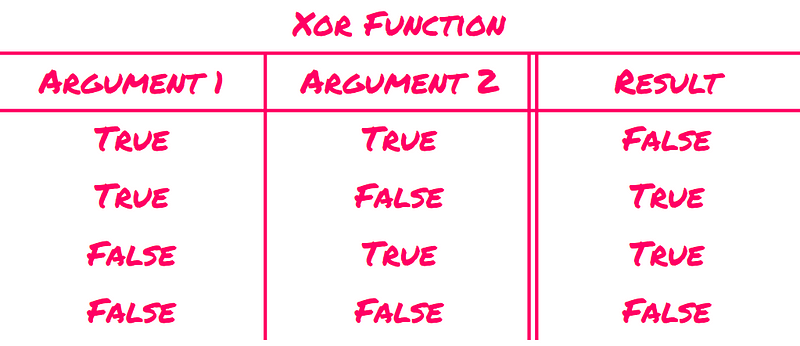
The XOR Function Distinction

In the case of XOR, if we change the false value in the second row to true, both inputs become true, mirroring the first row, yet the output is false. Thus, the output can switch from true to false when an input transitions from false to true, indicating that XOR is not monotonic.

Now, how many monotonic Boolean functions exist with two inputs? The total count of Boolean functions (regardless of monotonicity) with two inputs is 16. Since each of the two inputs can take on two values, this results in 2² = 4 combinations. For each combination, the output can also be either of two values, leading to 2? = 16 possible functions.

While we could examine all of these functions to tally the monotonic ones, I can simply provide the answer: there are 6. This leads to the Dedekind Number for two arguments, denoted as M(2) = 6.

Exploring M(3)

What about M(3)? This represents monotonic Boolean functions with three inputs. For example:

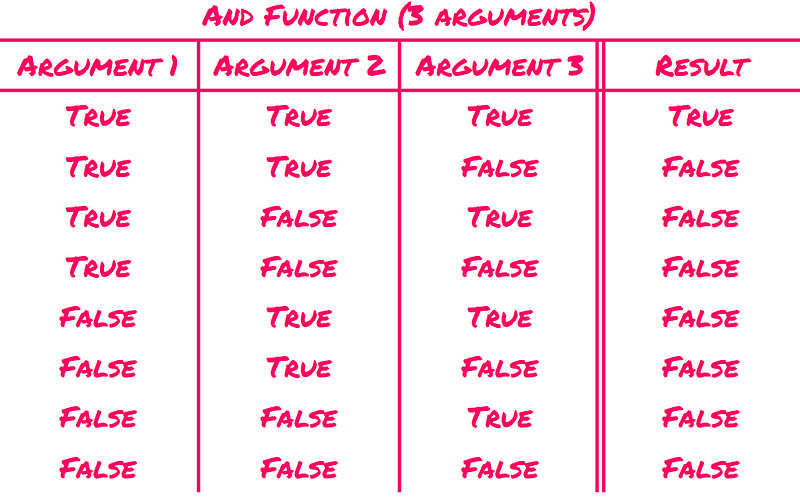
The AND Function with Three Inputs

The total number of Boolean functions with three inputs amounts to 2? = 256, which is a significant increase compared to the 16 functions available with two inputs. Out of these, 20 are monotonic, so we have M(3) = 20.

The number of Boolean functions grows exponentially as more inputs are added: 2, 4, 16, 256, 65536, and so on, with each number (except 2) being the square of the previous one. This rapid increase is noteworthy.

It may not be surprising, then, that Dedekind Numbers also escalate quickly with the addition of inputs. M(7) equals 2414682040998, and M(8) is 56130437228687557907788, which exceeds 5 * 10²²—far surpassing the total number of grains of sand on Earth.