Section 1.1: The Basics of Random Walks

A random walk represents a fundamental stochastic process that can be simulated. It is characterized by the position of a particle or object, denoted as ( x ) in an ( n )-dimensional space, which is updated by adding a random vector ( Delta r ). In simpler terms, we can numerically create a random walk through a recursive equation like the one shown below:

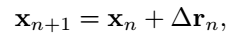
In this equation,

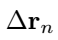
is a random variable sampled at each integer ( n ). This variable can adopt various forms, such as a normal random variable, a Poisson variable, or even a uniform random variable. The choice of distribution depends on the specific application. For instance, if you aim to model random walks resembling “Brownian motion”—the erratic movement often observed in natural stochastic processes like stock prices or the motion of particles in heated liquids—you would typically select a normally distributed variable:

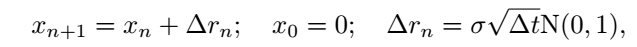
In this context, ( Delta t ) indicates the time step, representing the intervals between time values, while ( sigma ) controls the variance of the step ( Delta r ). The term ( N(0,1) ) symbolizes a standard normal random variable with a mean of zero and a variance of one, sampled at each step. The process begins with an initial value, such as ( x_0 = 0 ), and we iteratively add values based on the equation within a for-loop.

Here’s an example of MATLAB code that simulates multiple independent random walks:

---

% A simple random walk simulator in 1-dimension

%

% Created by: Oscar A. Nieves

% Updated: 2021

---

close all; clear all; clc;

%% Parameters

T = 0.5; % total simulation time

sims = 5; % number of independent simulations

dt = 1e-3; % step size

tv = 0:dt:T; % array of time values

x0 = 0; % starting position

sigma = 0.2; % variance parameter

Lt = length(tv);

Y = zeros(Lt,sims); % matrix for storing random walks

%% Random walk loop

% Generate multiple independent random walks

for N = 1:sims

x = zeros(Lt,1);

x(1) = x0;

for n = 1:Lt-1

Dr = sigma*sqrt(dt).*normrnd(0,1);

x(n+1) = x(n) + Dr;

end

Y(:,N) = x;

end

%% Plotting results

figure(1);

set(gcf,'color','w');

plot(tv,Y,'LineWidth',3);

xlabel('Time (s)');

ylabel('x(t)');

title('Random Walk Simulation');

set(gca,'FontSize',20);

---

Executing this MATLAB code will yield a plot similar to the one depicted in Figure 1.

As illustrated, all walks commence from the same initial point but diverge into distinct paths over time. The degree of randomness is influenced by both the time step ( Delta t ) and the parameter ( sigma ).

In addition to the normal distribution, we can also create random walks using other probability distributions. For instance, if we want the random step to follow a Poisson distribution, we would write:

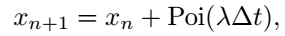
In this scenario, ( Poi(...) ) represents a Poisson random variable with a specified mean. By slightly adjusting our previous MATLAB code to incorporate this random step instead of the normal random variables, we could create simulations like the one depicted in the following image:

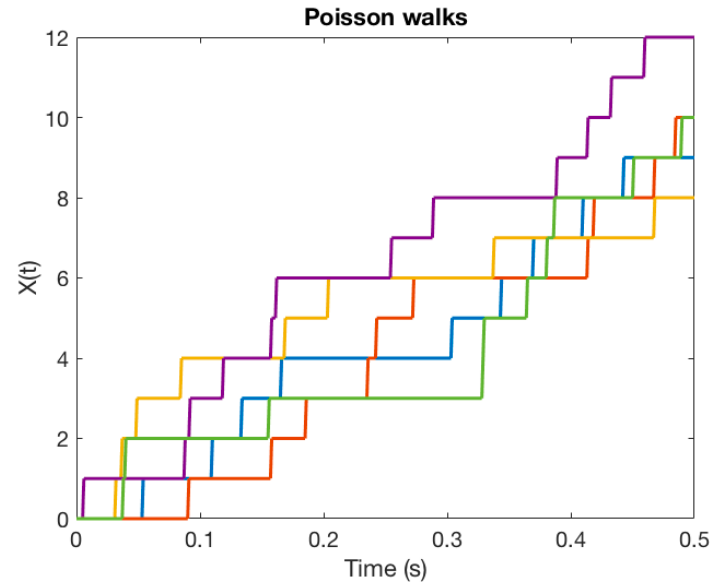
Figure 2: Multiple independent Poisson random walks.

To summarize, random walks can be effectively simulated using recursive relationships, where a random step with defined statistical properties is employed to update the next value of our stochastic process ( x(t) ).