Understanding Differentiation: The Essence of dy/dx in Calculus
Written on
Chapter 1: Introduction to Differentiation
Differentiation is a crucial concept in calculus, representing the process of calculating the ratio dy/dx, where 'y' is the dependent variable and 'x' is the independent variable. This ratio is particularly important as it examines the behavior of 'y' as 'x' changes, specifically in the limit where both 'dy' and 'dx' approach infinitesimally small values.
For those who might find these ideas challenging, fear not; I’ll provide a straightforward illustrated example in the following sections. This essay will first lay out the conceptual framework before diving into practical applications. As this is the fifth installment in my calculus series, I suggest reviewing the previous essays for a more comprehensive understanding.
Section 1.1: Why is dy/dx Important?
Many students of calculus accept the ratio dy/dx without question. However, it’s essential to understand its significance. At its core, calculus addresses the concept of change. While some might describe dy/dx as the slope of the change being analyzed, I prefer to view it differently.
The ratio dy/dx illustrates how the dependent variable 'y' responds to changes in the independent variable 'x'. In my prior essay on derivatives, I discussed how 'dy' and 'dx' represent infinitesimally small changes in 'y' and 'x', respectively. Thus, dy/dx conveys how 'y' varies concerning 'x' when 'x' undergoes a minuscule change.
Historically, this ratio was referred to as the differential coefficient, a term that has since fallen out of favor. Today, we simply call it the derivative. With that established, let’s delve into the process of differentiation.
Section 1.2: The Concept of Differentiation
Let's examine the function: y = f(x) = x²
Assuming positive values for both 'x' and 'y', it becomes evident that as 'x' increases, 'y' also increases correspondingly. To conceptualize this idea, let us increase 'x' by an infinitesimal amount, denoted as 'dx'. Consequently, 'y' will increase by a corresponding infinitesimal amount 'dy', expressed as follows:
y = x² ? y + dy = (x + dx)²
Applying the binomial theorem yields: y + dy = x² + 2xdx + (dx)²
Notice that the term (dx)² is an infinitesimal of a higher order. This is why we can disregard it, leading us to:
y + dy = x² + 2xdx
Subtracting 'y' from both sides, where y = x², we arrive at:
? dy = 2xdx
Dividing both sides by 'dx' gives us: dy/dx = 2x
Thus, the derivative of y = x² with respect to 'x' is 2x. But what does this signify? Let’s explore this through a numerical example.
Section 1.3: Illustrated Example of Differentiation
Suppose x = 1000, resulting in y = x² = 1,000,000. If we consider an infinitesimal increase in 'x', let’s set dx = 1. Then, using our original equation, we can calculate the new value of 'y':
y + dy = (1000 + 1)² = 1,002,001
Ignoring the negligible second-order term (1²), we find: dy = 2000.
Since we initially chose dx = 1: dy/dx = 2000/1 = 2000 = 2*1000 = 2*x.
To further illustrate, let’s change dx to 0.1. Now our equation modifies to:
y + dy = (1000 + 0.1)² = 1,000,200.01
In this case, the higher-order term we neglect is 0.01. Thus, we compute the derivative:
dy/dx = 200/0.1 = 2000 = 2*1000 = 2*x.
Even with a reduced dx, we consistently arrive at the same result. The brilliance of calculus lies in reducing 'dx' closer to zero, leading us to the concept of limits.
Chapter 2: Differentiation through Limit Theory
Mathematicians often use the Greek letter delta (Δ) instead of 'd' to denote infinitesimally small quantities. In limit theory, the derivative is defined as the limit of the ratio dy/dx as Δx approaches zero. This can be represented mathematically as follows:
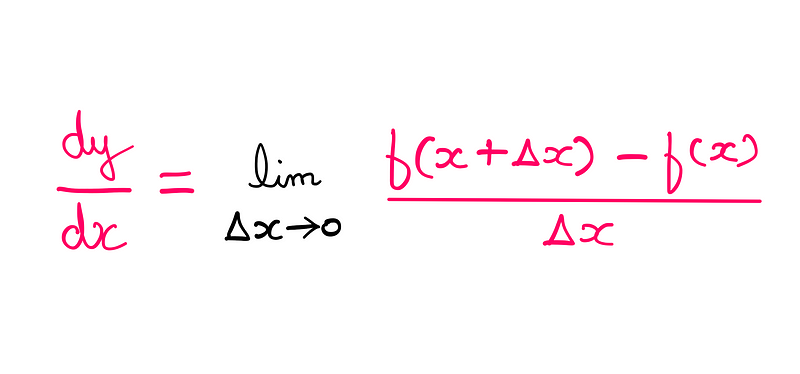
For the function f(x) = 8x, we derive:
Δy/Δx = (8*Δx)/Δx
As Δx approaches zero, the limit of Δy/Δx equals 8. Hence, the derivative of y = f(x) = 8x is 8 with respect to 'x'.
I hope this essay has clarified the essentials of differentiation. In my next installment, I will expand on these concepts and introduce another valuable tool in calculus: the power rule.
For additional resources and a comprehensive overview of my work, please visit my about page. If you appreciate my content, consider supporting me on Patreon.
Reference and credit: Silvanus Thompson.
The first video, "Differentiation," offers insights into the concept and methodology of differentiation in calculus.
The second video, "What is the Difference Between dy/dx and d/dx," clarifies the distinctions and applications of these fundamental terms in calculus.