Was Mathematics in 1858 Simpler or More Challenging?
Written on
Chapter 1: Historical Context of Mathematics Education
Recently, I came across some intriguing examination questions from the inaugural national exams conducted by The University of Cambridge Local Examinations Syndicate in 1858. This topic often ignites discussions about whether modern mathematics curricula and assessments have become easier or more difficult. To explore this, I will examine several questions from those exams.
The first two inquiries were designed for 'Junior' candidates, aged 16 and younger, while the subsequent two targeted 'Senior' candidates, aged 18 and younger. I will present my solutions for each, although I will refrain from solving the last one for Junior candidates—there's a reason for that.
It's essential to consider that in 1858, it was uncommon for children to attend school at the age of 16, let alone 18. Most working-class children had no access to education, with only a select few attending charitable schools that provided basic education. By age 10, many of these children were compelled to work full-time in manual labor, such as agriculture, mining, or textiles.
Education was predominantly the privilege of the affluent, so these questions were likely presented only to upper-class children who benefited from private schooling and tutoring. Furthermore, it is worth noting that only boys participated in math classes, as the education of upper-class girls focused on subjects deemed more suitable for preparing them for their future roles as wives.
Reform in education was sluggish in Britain. Compulsory attendance for children under 10 was not enforced until 1880, with the age raised incrementally to 16 by 1972.
Section 1.1: Question 1 — Junior Candidates
The first question posed was: “If workmen can complete a task in one week by working 11 hours a day for 6 days, how many hours must they work each day to achieve the same result if they take half of Saturday off but work 1/12 more efficiently per hour?”
My approach to solving this involved some complex arithmetic, especially considering the absence of calculators in 1858. I set up the problem algebraically: Let w be the work rate per hour. The total work completed in the first scenario can be expressed as 66w (six days at 11 hours each).
In the second scenario, where they work 5.5 days and 1/12 more efficiently, the total work done becomes (13w)/12 multiplied by the unknown hours per day, which I will denote as x. By equating the two scenarios, I arrive at x = 792/71.5. After employing long division, my final answer is approximately 11.077 hours per day, rounded to three decimal places.
Subsection 1.1.1: Question 2 — Junior Candidates
The second question states: “The difference between two numbers is 3, and the difference of their cubes is 279. Find the numbers.”
This problem can be approached in several ways, but trial and error might prove tedious. I assumed the numbers represented positive integers. Let x and y be the numbers. We know that x - y = 3 and x³ - y³ = 279. By factoring, we obtain x³ - y³ = (x - y)(x² + xy + y²), leading to x² + xy + y² = 279/3 = 93.
Completing the square gives us (x + y)² = 93 + xy. After some educated guessing, I found that x = 7 and y = 4 satisfy the conditions.

Section 1.2: Question 3 — Senior Candidates
The third question requires knowledge of multiplying terms and handling indices. It's straightforward, and I believe the solution is not particularly challenging.
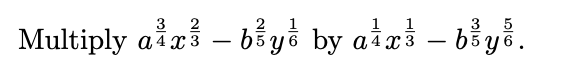
Chapter 2: Modern Perspectives on Historical Math
The first video explores the challenges of learning math as a senior citizen, shedding light on the barriers that age can impose on understanding complex subjects.
The second video contrasts old school math with new school methods, providing insights into how teaching and learning approaches have evolved over time.
Section 2.1: Question 4 — Senior Candidates
The fourth question involves expressions known as surds in the UK. These have long been part of math education and often pose challenges for students. However, I find them quite enjoyable. The task requires manipulation of the expression to simplify it.
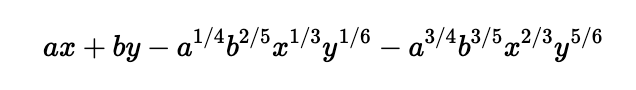
Reflecting on these questions, it appears that there wasn't a significant distinction between the expectations for 16-year-olds versus those for 18-year-olds in 1858. The Junior questions would be considered moderate to challenging by today's GCSE standards, while the Senior questions seem equally accessible, failing to match the rigor of current A-level examinations.
Let’s conclude with a fifth question from the 1858 papers, which I won’t attempt to solve: “Draw, from memory, a wheelbarrow turned upside down.” How would you approach these historical math questions? Feel free to share your thoughts.